Scraping Dynamic Pages with Scrapy + Selenium

May 14, 2018

If you already know how to set up Scrapy and Selenium, skip to the Integration section to see how to integrate the two.

The final code can be viewed here.

Overview
Scrapy
Selenium
Integration
Alternatives

Overview

Scrapy is a python framework used for scraping websites, but a common problem is finding a way to get data off of a site that is dynamically loaded. Many websites will execute JavaScript in the client's browser, and that JavaScript will grab data for a webpage. Scrapy does not have the ability to execute this JavaScript.

Selenium is a tool that automates web browsers for testing purposes, but it can be used along with Scrapy to load all of a site's data whenever Scrapy sends a request.

Lets say we want to scrape Twitch for the currently featured stream. There is probably a way to do it through the API, but lets pretend there isn't.

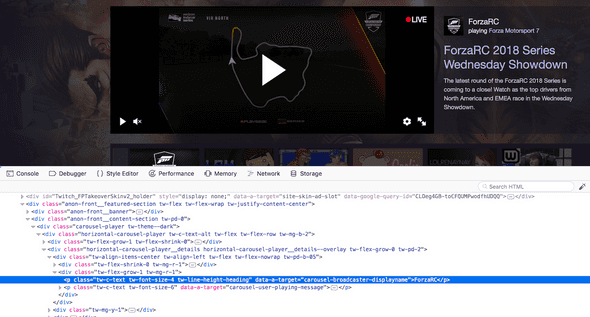
To start we can go to Twitch and inspect the page through your browser and see what the HTML looks like.

You'll probably see something like this...

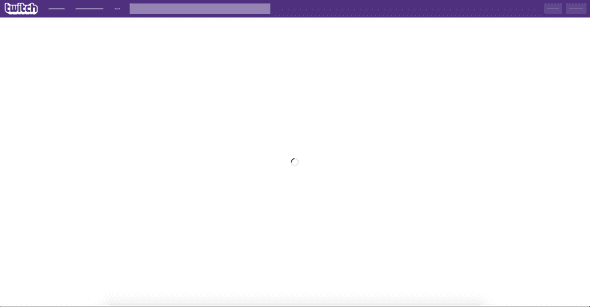
pretty much all the data you see on twitch is loaded through JS. Without it you would just get a blank page with a loading icon like this...

So we are going to need to use Scrapy and Selenium to get the data we want.

Scrapy

To set up your dev environment install scrapy.

pip install scrapy

Make sure to check the documentation here

Then create scrapy's files.

scrapy startproject twitch_featured

Now we are going to create a spider to crawl twitch.

Go to your spiders directory.

cd twitch_featured/twitch_featured/spiders

And create a new spider twitch.py

import scrapy


class TwitchSpider(scrapy.Spider):
    name = 'twitch-spider'
    start_urls = [
        'https://twitch.tv',
    ]

    def parse(self, response):
        pass

Scrapy will send a request to each url in start_urls and pass the response to the parse method.

Right now we aren't doing anything with Twitch's response, so lets use scrapy selectors to get data off of the page.

def parse(self, response):
    streamer = response.xpath(
        '//p[@data-a-target="carousel-broadcaster-displayname"]/text()'
    ).extract()
    playing = response.xpath(
        '//p[@data-a-target="carousel-user-playing-message"]/span/a/text()'
    ).extract()

    yield {
        'streamer': streamer,
        'playing': playing
    }

We are giving scrapy an xpath, and it uses that to grab the text that tells you the broadcaster's displayname and current game.

For more information about how xpaths work, look at this tutorial.

To test our code we can run...

scrapy crawl twitch-spider -o output.json

We are telling the twitch-spider to crawl it's URLs and send the data it scrapes to output.json file.

But the output.json file is empty because we havn't added Selenium yet. The data we want isn't there.

Selenium

Selenium requires a pre existing browser to be installed. More specifically the driver for a browser. For this tutorial I'll be using this Chrome driver. The documentation for what else Selenium supports can be found here

Install Selenium with pip

pip install selenium

Integration

Now that we have Scrapy set up and Selenium installed, we need to integrate the two together.

I will be puting the Selenium code in the DownloaderMiddleware. The methods in this class are called whenever Scrapy makes a request. It modifies the request/response in some way, and passes it back to Scrapy.

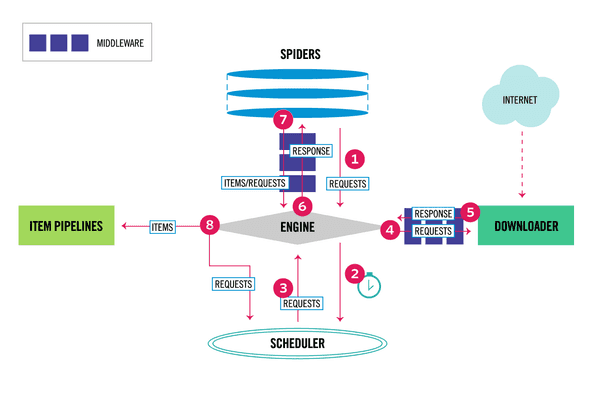
This diagram explains the steps Scrapy takes.

We are going to be putting code right after step 4 that makes the request through Selenium, and then we'll pass back what Selenium loads as step 5.

First we need to activate the downloader middleware class. Search settings.py for this code, and uncomment it.

# DOWNLOADER_MIDDLEWARES = {
#     'twitch_featured.middlewares.TwitchFeaturedDownloaderMiddleware': 543,
# }

Open up the middlewares file located at twitch_featured/twitch_featured/middlewares.py

Outside of the middleware classes, initialize the Selenium driver

...
from scrapy import signals
from scrapy.http import HtmlResponse
from selenium import webdriver

options = webdriver.ChromeOptions()
options.add_argument('headless')
options.add_argument('window-size=1200x600')

driver = webdriver.Chrome(chrome_options=options)
...

Then look for the TwitchFeaturedDownloaderMiddleware class, and the process_request method.

if request.url != 'https://www.twitch.tv/':
    return None

driver.get(request.url)

body = driver.page_source
return HtmlResponse(driver.current_url, body=body, encoding='utf-8', request=request)

process_request is called anytime scrapy makes a request. The code we added tells Selenium to make the request to https://www.twitch.tv/ through the Chrome driver, get the page_source of the response, and then we return that as a Scrapy HtmlResponse.

The code in Scrapy to make a request is unchanged, we are just making the request go through Selenium, and executing any dynamic content.

Running Scrapy now will most likely work. It will output some json that contains the featured streamer's name and game. The reason it may not work is that Twitch has a lot of JavaScript to execute. In fact it is continuously executing JavaScript. Selenium only lets the page load for a certain time, and the data we want might not have loaded in time.

One way to fix this is to tell Selenium to wait until the element we want is loaded.

Add these imports in middlewares.py

from selenium.webdriver.common.by import By
from selenium.webdriver.support.ui import WebDriverWait
from selenium.webdriver.support import expected_conditions as EC

And add this code to process_request

def process_request(self, request, spider):
  if request.url != 'https://www.twitch.tv/':
      return None

  driver.get(request.url)
  WebDriverWait(driver, 10).until(
      EC.presence_of_element_located((By.XPATH, "//p[@data-a-target='carousel-broadcaster-displayname']"))
  )

  body = driver.page_source
  return HtmlResponse(driver.current_url, body=body, encoding='utf-8', request=request)

We used the same xpath as before, and we told Selenium to wait until the element we are looking for is loaded, or if it hasn't after 10 seconds to throw an exception.

It's important to note that Scrapy will make additional requests to a various endpoints, and to make sure you are only using Selenium on the actual request to twitch. This is done in the first lines of process_request where we check the request url.

Adding additional code to tell Selenium to wait is usually not necessary. It depends on how long the page you are scraping takes to load.

Now if we run our code

scrapy crawl twitch-spider -o output.json

and look in output.json, you should see something like this...

[
{"streamer": ["ForzaRC"], "playing": ["Forza Motorsport 7"]}
]

Alternatives

If you would like to scrape your page using Selenium library, you could move the code from the downloader middleware to your spider, and manually make your requests there. This may require some manipulation of how Scrapy handles requests so that you don't make two requests, one through Scrapy and one through Selenium.

By putting it in your downloader middleware it lets you keep using Scrapy normally, and not have to worry about setting up Selenium for each spider.